

В научных исследованиях математические формулы и объекты играют важную роль при представлении и анализе данных. Один из самых популярных инструментов для создания и форматирования таких формул — Microsoft Word. С его помощью вы можете легко вставлять, редактировать и представлять вашу математическую информацию.
В Microsoft Word вы можете использовать различные типы формул, включая уравнения, интегралы, дроби, матрицы и многое другое. Вы также можете добавлять специальные символы и операторы, такие как загромождающие индексы и указатели. Завершите вашу формулу с помощью правильной нотации и значений, и ваша математическая информация будет четко и последовательно представлена.
Кроме того, Microsoft Word предлагает широкий выбор функций для форматирования и стилизации математических формул. Здесь вы можете изменять размер шрифта, цвет, стиль и выравнивание формулы. Вы также можете добавить подписи и ссылки на формулы, чтобы облегчить чтение и понимание вашего научного текста.
По мере того, как вы работаете над научным исследованием, Microsoft Word предоставляет вам инструменты для автоматического редактирования и обновления формул. Если вы измените значения или условия в вашей формуле, программа автоматически пересчитает и обновит все связанные элементы, что помогает избежать ошибок или несоответствий.
В целом, использование формул и математических объектов в Microsoft Word значительно упрощает процесс создания и форматирования научных исследований. Этот инструмент позволяет четко и последовательно представлять математическую информацию, делая вашу работу более понятной и профессиональной.
Примеры использования формул и математических объектов в Microsoft Word для научных исследований
Microsoft Word предоставляет мощные инструменты для создания и редактирования математических формул в научных исследованиях. С помощью различных функций и инструментов, исследователи могут удобно вставлять и форматировать формулы, облегчая понимание и представление комплексных математических концепций.
- Уравнения: Математические уравнения часто используются в научных исследованиях для формализации концепций и выражения закономерностей. В Microsoft Word можно использовать функцию Equation для создания сложных уравнений с использованием различных математических операций, символов и переменных. Это упрощает представление и понимание математических моделей и формул в научных публикациях.
- Матрицы и векторы: Векторы и матрицы широко используются в различных областях научных исследований, таких как физика, статистика, информатика и многих других. В Microsoft Word можно легко создавать и редактировать матрицы и векторы с помощью функции Equation. Это позволяет удобно представлять многомерные данные и математические конструкции в тексте и диаграммах.
- Дифференциальные уравнения: В научных исследованиях, особенно в физике, биологии и инженерии, дифференциальные уравнения играют важную роль в моделировании и анализе различных процессов и явлений. В Microsoft Word можно использовать специальные функции и инструменты, такие как Equation Editor, для создания и решения дифференциальных уравнений. Это позволяет исследователям наглядно представлять и анализировать динамику систем и процессов.
Все эти возможности Microsoft Word позволяют исследователям удобно представлять и объяснять сложные математические концепции в научных публикациях. Они упрощают создание и форматирование формул и математических объектов, делая текст более читабельным и понятным для читателей. Это существенно облегчает передачу идей и результатов исследований в научном сообществе.
Создание математических формул в Microsoft Word
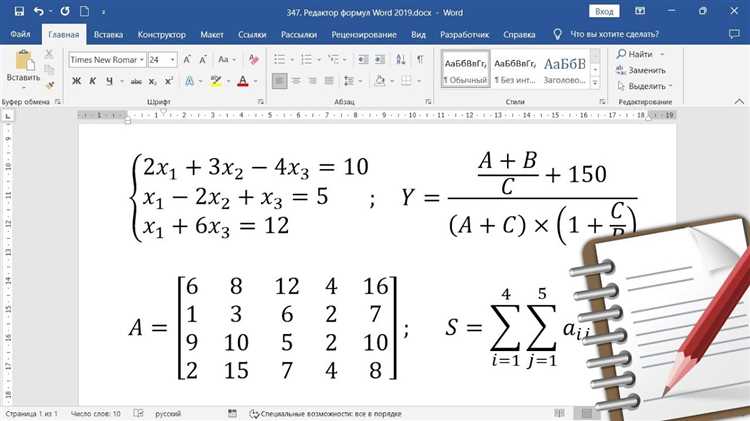

Редактор уравнений в Word позволяет создавать различные математические символы, операторы и функции. С помощью специальной визуальной панели инструментов можно выбрать нужный символ или оператор и вставить его в формулу. Для упрощения создания сложных формул редактор предоставляет возможность использовать автоматическую подстановку символов и операторов.
Математические формулы в Word могут быть различной сложности и содержать различные элементы, такие как дроби, индексы, верхние и нижние индексы, матрицы и многое другое. Редактор уравнений предлагает широкий набор инструментов для создания любых нужных элементов формулы, а также обеспечивает удобное размещение и выравнивание элементов.
Кроме того, в Word можно создавать сложные формулы с использованием символов переменных, констант и операторов. Для удобства набора формул редактор уравнений предоставляет специальные шаблоны и сокращения, а также функцию предварительного просмотра формулы перед ее вставкой.
В целом, создание математических формул в Microsoft Word является простым и удобным процессом, который значительно упрощает работу ученых и исследователей. Возможности редактора уравнений позволяют создавать формулы различной сложности, выравнивать и размещать элементы формулы и получать профессионально оформленные математические тексты.
Использование специальных символов и операторов в формулах
В научных исследованиях, особенно в области математики и физики, часто требуется использование специальных символов и операторов в формулах. Эти символы и операторы применяются для обозначения различных математических концепций, свойств и операций.
Символы, например греческие буквы, важны для обозначения переменных, параметров и констант в формулах. Например, символ дельта (Δ) используется для обозначения изменения или разности, а символ пи (π) – для обозначения числа пи.
Операторы, такие как сумма (Σ), произведение (∏), интеграл (∫) и дифференцирование (d/dx), позволяют выполнить различные математические операции над переменными и функциями в формулах. Например, сумма используется для обозначения суммирования ряда чисел или функций, а интеграл – для нахождения площади под кривой или значения определенного интеграла.
Использование специальных символов и операторов в формулах облегчает понимание и описание сложных математических выражений. Программа Microsoft Word предлагает широкий набор этих символов и операторов, которые могут быть вставлены в формулы с помощью специального редактора формул. Это позволяет создавать аккуратные и понятные математические выражения для научных исследований и публикаций.
Применение функций и переменных в математических формулах
В математических формулах функции и переменные играют важную роль, позволяя нам описать и изучить различные явления и зависимости. Функции представляют собой математические правила, которые преобразуют входные значения в выходные значения. Они могут быть использованы для моделирования сложных процессов, например, изменения температуры во времени или зависимости между различными переменными.
Переменные, с другой стороны, являются символами, представляющими неизвестные или изменяющиеся значения. Они могут быть использованы для обозначения различных величин, таких как длина, масса или время. Переменные позволяют нам создавать формулы, которые зависят от конкретных значений этих величин и становятся полезными инструментами для анализа данных и решения математических задач.
В Microsoft Word мы можем использовать функции и переменные в математических формулах с помощью специальных инструментов, таких как редактор формул. Этот инструмент позволяет нам создавать сложные математические выражения, используя различные функции и переменные, а затем вставлять их в документы Word.
Например, мы можем создать формулу, представляющую закон Гука, который описывает зависимость между силой, применяемой к упругому телу, и его деформацией. В этой формуле мы будем использовать переменные, такие как сила (F), коэффициент упругости (k) и длина тела (l). Затем мы можем применить формулу к различным значениям переменных, чтобы определить деформацию тела.
Интегрирование и дифференцирование в Microsoft Word
Для интегрирования формулы в Microsoft Word вы можете воспользоваться функцией «Вставить формулу». Каждое интеграл, необходимое основание и пределы интегрирования могут быть введены непосредственно в формулу. Word автоматически распознает формулу и отображает ее в соответствующем формате.
Чтобы дифференцировать формулу, вы можете использовать инструмент «Дифференцирование», который позволяет выделить часть формулы и применить к ней операцию дифференцирования. Это особенно полезно при создании научных исследований и математических документов, где требуются вычисления и применение дифференциальных операторов.
Используя данные возможности в Microsoft Word, вы можете легко вставлять, редактировать и форматировать формулы, интегрировать и дифференцировать их в своих научных исследованиях, документах или презентациях. Все это позволяет улучшить визуальное представление математических выражений и облегчить их понимание.
Использование матриц и векторов в научных исследованиях
Матрицы представляют собой двумерные прямоугольные таблицы чисел, которые состоят из строк и столбцов. Они могут быть использованы для описания систем линейных уравнений, преобразований и симметрий объектов, а также для моделирования физических и химических процессов. Векторы, с другой стороны, являются одномерными матрицами и используются для представления направления и интенсивности физических величин, таких как сила, скорость и ускорение.
Матрицы и векторы можно использовать для решения различных задач в научных исследованиях. Например, они могут быть использованы для анализа данных, обработки изображений, моделирования и оптимизации систем, а также для решения систем линейных уравнений и вычисления собственных значений и векторов. Они также широко применяются в математической статистике для оценки параметров и построения моделей.
Использование матриц и векторов облегчает работу с большими объемами данных и позволяет проводить сложные вычисления с высокой точностью. Они также способствуют более эффективному и структурированному представлению информации. Поэтому понимание и умение работать с матрицами и векторами являются важными навыками для исследователя в любой научной области.
Вопрос-ответ:
Какая роль матриц в научных исследованиях?
Матрицы широко используются в научных исследованиях для представления и обработки данных. Они позволяют компактно хранить информацию о больших массивах данных и выполнять различные операции над этими данными.
В чем преимущество использования векторов в научных исследованиях?
Использование векторов позволяет более эффективно оперировать многомерными данными. Векторы позволяют компактно хранить информацию и проводить операции, такие как сложение, умножение на скаляр и скалярное произведение.
Как матрицы и векторы используются в анализе данных?
Матрицы и векторы используются в анализе данных для представления и обработки многомерных данных. Они позволяют применять различные статистические методы и алгоритмы машинного обучения, такие как линейная регрессия, кластеризация и разложение на собственные значения.
Как матрицы и векторы помогают в решении математических задач?
Матрицы и векторы используются для формулировки и решения математических задач. Они позволяют записать системы уравнений в матричной форме и применять методы решения, такие как метод Гаусса или метод наименьших квадратов. Векторы также используются для представления геометрических объектов, таких как векторные пространства и фигуры.
Какие научные области часто используют матрицы и векторы?
Матрицы и векторы широко применяются во многих научных областях, включая физику, химию, биологию, экономику и информатику. Они используются для моделирования систем, анализа данных, решения уравнений и многих других задач. Матрицы также используются в компьютерной графике и обработке изображений.
Какие преимущества есть у использования матриц и векторов в научных исследованиях?
Использование матриц и векторов позволяет исследователям компактно представлять и обрабатывать большие объемы данных. Матрицы и векторы удобны для работы с многомерными данными, например, при анализе геномов или изображений. Кроме того, матрицы и векторы широко применяются в линейной алгебре и статистике, что позволяет исследователям проводить сложные математические операции и моделирование.
Какие методы можно применять при использовании матриц и векторов в научных исследованиях?
При использовании матриц и векторов в научных исследованиях можно применять различные методы, такие как метод главных компонент, факторный анализ, кластерный анализ и многое другое. Матрицы и векторы также удобны для решения систем линейных уравнений, определения собственных значений и собственных векторов, аппроксимации и регрессионного анализа. Благодаря этим методам исследователи могут выявить скрытые закономерности, классифицировать данные и делать выводы на основе математических моделей.

